Finding End Effector Position

This math allows the robot to translate velocity requirements in the global coordinate frame of x and y to velocities of the ropes. We first defined two coordinate systems and gave names to the various names and angles in the diagram:

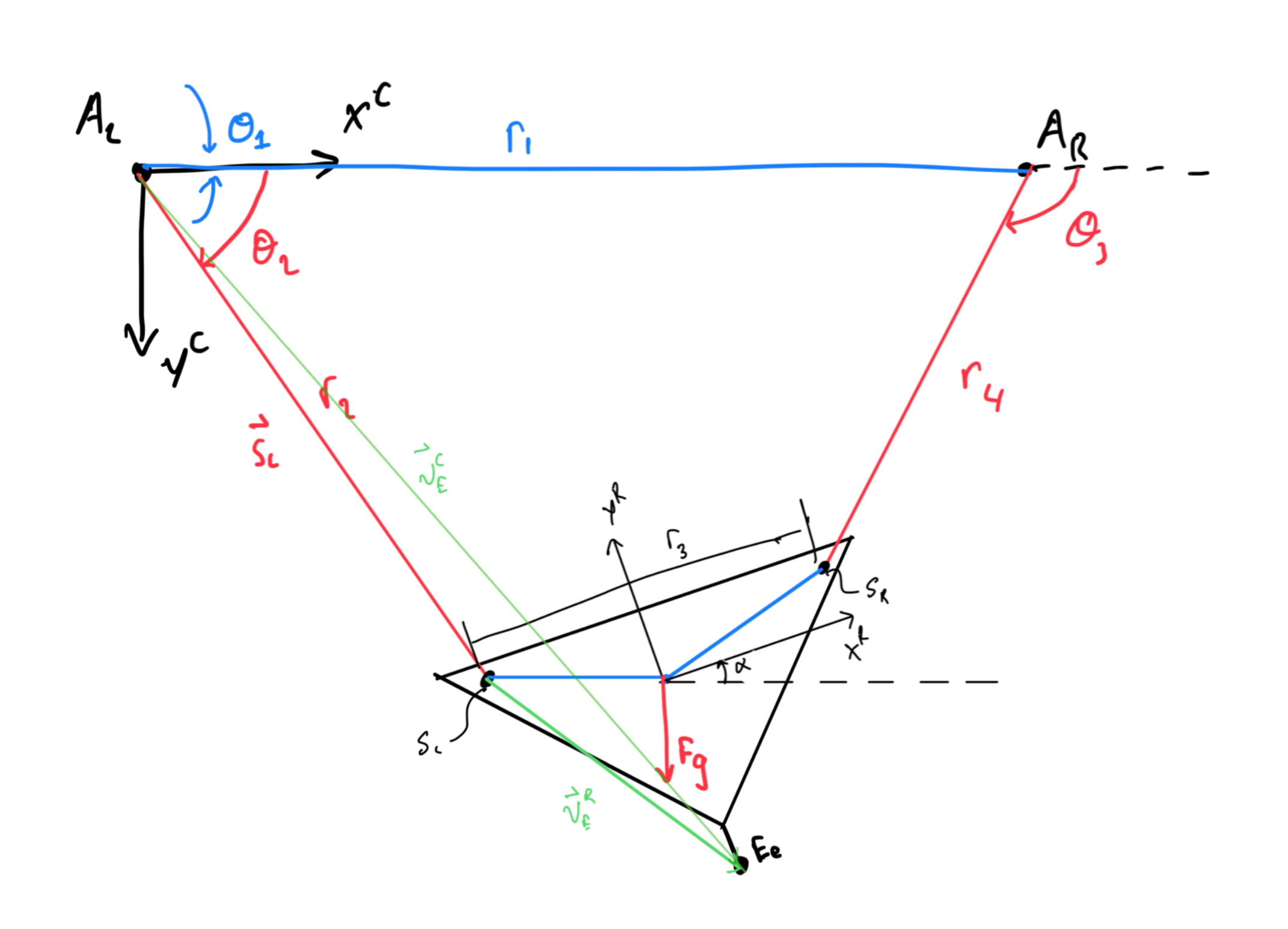
Here, $X^C$ and $Y^C$ make up the canvas coordinate frame. This is intentionally chosen to be the same orientation as the coordinate system in images. $Y^C$ is chosen so its parallel to the gravity vector. $X^R$ and $Y^R$ define the coordinate system that moves with the robot, located at the robot’s centre of gravity.

There are a few values that are constant and known beforehand:

• $r_1$: The distance between the pegs that Opus is hanging off of
• $r_3$: The distance between the apertures where the rope comes out of on Opus
• $r_L$, $r_R$: The vector between the centre of gravity and the apertures defined in the $X^RY^R$ frame
• $F_g$: The force of gravity

$\alpha$ is the angle of the robot’s frame relative to the wall’s frame. $\alpha$ is typically not known, but we designed Opus with an IMU. This allowed us to use an Attitude Heading Reference System Kalman Filter (AHRS) to get stable $\alpha$ values from the device. We use the output of the AHRS Kalman Filter as a known $\alpha$ value.

For a given location in the $X^C$, $Y^C$ frame, we need to find the lengths $r_2$ and $r_4$ that result in it.

This looks suspiciously like a four bar linkage, with the added constraint that beams $r_2$ and $r_4$ cannot be in compression, since they are cables. Therefore, the four-bar linkage governing formula from Fundamentals of Machine Theory and Mechanisms was used as a starting point, and we came to the following formulae:

Givens:

Due to the $y$ position being the same on the anchors: $\theta_1 = 0$

Formula:

To compute $\theta_2$ and $\theta_4$, we use the AHRS determined angle $\theta_1$ and the current lengths of the cables ($r_2$, $r_4$).

$$ \begin{align} x_3 &= r_1\cos{\theta_1} - r_3\cos{\alpha} \\ y_3 &= r_1\sin{\theta_1} - r_3\sin{\alpha} \end{align} $$

$$ % \DelcareMathOperator{\atantwo}{atan2} \begin{align} \theta_4 &= \text{atan2}(y_3, x_3) + \arccos\left({\frac{x_3^2 + y_3^2 + r_4^2 - r_2^2}{-2r_4\sqrt{x_3^2 + y_3^2}}}\right) \\ \theta_2 &= \text{atan2}\left(\frac{y_3 + r_4\sin\theta_4}{r_2}, \frac{x_3 + r_4\cos\theta_4}{r_2}\right) \end{align} $$

With $\theta_2$, we can get the position of the left spool exit point quite easily: $$\vec{S_L} = r_2\begin{bmatrix} \cos{\theta_2} \\ -\sin{\theta_2} \end{bmatrix} $$

Finally, the end effector position can be determined by rotating the vector $\vec{V_E^R}$ that is defined in the robot’s coordinate frame by $-\alpha$ radians, and adding it to $\vec{S_L}$:

$$ \vec{V_E^C} = \vec{S_L} + \begin{bmatrix} \cos\left({-\alpha}\right) & -\sin\left({-\alpha}\right) \\ \sin\left({-\alpha}\right) & \cos\left({-\alpha}\right) \end{bmatrix} \vec{V_E^R} $$